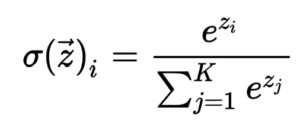First Published 12 June 2023

Introduction:

Often used in machine learning and deep neural networks, the softmax function is a crucial tool that plays a fundamental role in transforming raw output into meaningful probability distributions. By converting a set of arbitrary values into probabilities, the softmax function enables researchers to make decisions and predictions based on the relative strength of these probabilities. In this blog post, we will dive deep into the concept of the softmax function including the mathematics behind it and its applications. Hopefully this concept appeals to you as both useful and interesting.

What is the Softmax Function?

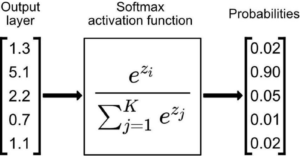
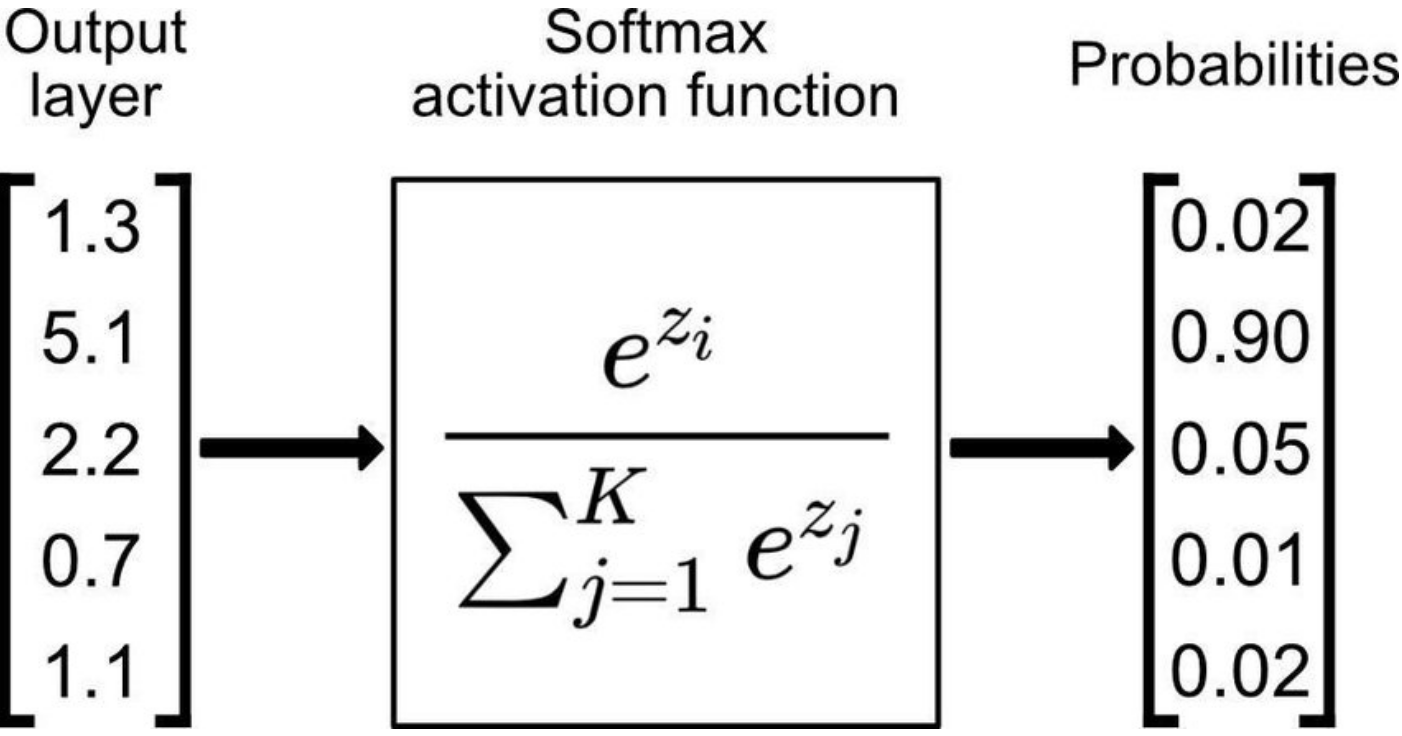
The softmax function, also known as the normalized exponential function, is a mathematical function that takes in a vector of real numbers and outputs a probability distribution over the elements of the vector. The function takes its name from the fact that it produces soft, or smooth, probabilities that all sum up to one. Softmax is particularly useful when dealing with multi-class classification problems, where we want to assign a probability to each class.

Mathematical Formula:

Given an input vector z = [z₁, z₂, …, zk], the softmax function transforms the values into a probability distribution vector σ = [σ₁, σ₂, …, σk]. The probability σi for each element zi is calculated as follows:

for j = 1 to k.

Here, exp denotes the exponential function, and the denominator represents the sum of the exponentials of all elements in the vector z.

Understanding the Softmax Function:

The softmax function takes the raw values in the input vector and sorts them into the range [0, 1], while ensuring that their sum remains 1. Softmax magnifies the differences between them, highlighting the most prominent elements in the distribution. For example, the standard softmax of (1, 2, 8) is approximately (0.001, 0.002, 0.997). This property makes softmax well-suited for tasks where we need to determine the most probable class among multiple options.

How Do We Interpret the Softmax Function?

The output of the softmax function can be interpreted as probabilities. Each element oi in the output vector represents the probability of the corresponding class i being the correct one. The class with the highest probability is typically chosen as the predicted class. Furthermore, the relative differences between the probabilities can provide valuable insights into the model’s confidence in its predictions. A higher probability indicates a more confident prediction, while lower probabilities imply more uncertainty.

References:

https://en.wikipedia.org/wiki/Softmax_function

https://deepai.org/machine-learning-glossary-and-terms/softmax-layer